Occasionally when working with customers on power supply
applications that require sourcing and sinking current which can be addressed
with the proper choice of a two-quadrant power supply, I am told “we need a
four-quadrant power supply to do this!” I ask why and it is explained to me
that they want to sink current down near or at zero volts and it requires
4-quadrant operation to work. The reasoning why is the case is illustrated in
Figure 1.
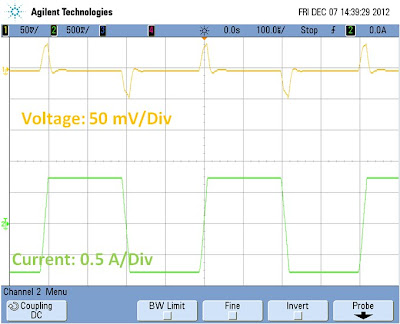
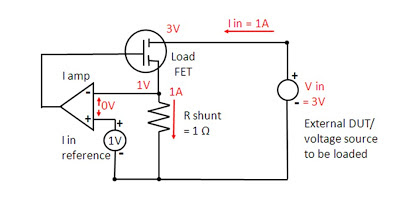
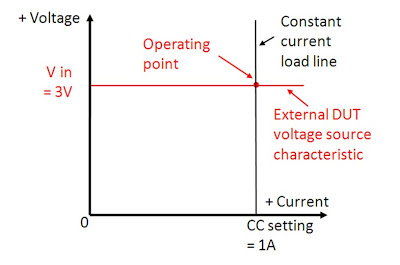
As can be seen in the diagram, in practical applications
when regulating a voltage at the DUT when sinking current, the voltage at the
power supply’s output terminals will be lower than the voltage at the DUT, due
to voltage drops in the wiring and connections. Often this means the power
supply’s output voltage at its terminals will be negative in order to regulate
the voltage at the DUT near or at zero volts.
Hence a four-quadrant power supply is required, right? Well,
not necessarily. It all depends on the choice of the two-quadrant power supply
as they’re not all the same! Some two-quadrant power supplies will regulate
right down to zero volts even when sinking current, while others will not. This
can be ascertained from reviewing their output characteristics.
Our N6781A, N6782A, N6785A and N6786A are examples of
some of our two-quadrant power supplies that will regulate down to zero volts
even when sinking current. This is
reflected in the graph of their output characteristics, shown in Figure 2.
Figure 2: Keysight N6781A, N6782A, N6785A and N6786A
2-quadrant output characteristics
What can be seen in Figure 2 is that these two-quadrant
power supplies can source and sink their full output current
rating, even along the horizontal zero volt axis of their V-I output
characteristic plots. The reason why they are able to do this is because
internally they do incorporate a negative voltage power rail that allows them
to regulate at zero volts even when sinking current. While you cannot program a
negative output voltage on them, making them two-quadrants instead of four,
they are actually able to drive their output terminals negative by a small
amount, if necessary. This will allow them to compensate for remote sense
voltage drop in the wiring, in order to maintain zero volts at the DUT while
sinking current. This also makes for a more complicated and more expensive
design.
Our N6900A and N7900A series advanced power sources (APS)
also have two-quadrant outputs. Their output characteristic is shown in Figure
3.
Figure 3: Keysight N6900A and N7900A series 2-quadrant
output characteristics
Here, in comparison, a certain amount of minimum positive
voltage is required when sinking current. It can be seen this minimum positive
voltage is proportional to the amount of sink current as indicated by the sloping
line that starts a small maximum voltage when at maximum sink current and
tapers to zero volts at zero sink current. Basically these series of 2-quadrant power
supplies are not able to regulate down to zero volts when sinking current.
The reason why is because they do not have an internal negative power voltage
rail that is needed for regulating at zero volts when sinking current.
So when needing to source and sink current and power near
or at zero volts do not immediately assume a 4-quadrant power supply is
required. Depending on the design of a 2-quadrant power supply, it may meet the
requirements, as not all 2-quadrant power supplies are the same! One way to
tell is to look at its output characteristics.